|
Different uses for voting
need different types of voting. |
 |
STV Protects |
 |

|
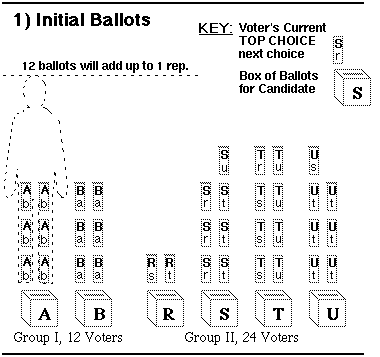
If the election shown below were decided by a plurality rule, the minority would get no representation. These rules give each voter 1 or more votes. A voter may give only 1 vote to each favorite candidate. The 3 candidates who get the most votes win. It is simple... and simplistic. The result has more to do with an interest group's ratio of voters to candidates than with its number of voters. If a group has too many candidates, their votes are divided and all lose. The initial ballots below gave 6 (first-place) votes to each candidate in Group I. They gave 2, 7, 8, and 7 votes to the candidates in Group II. The top 3 vote getters are all in Group II so it wins all the seats. This is the simplest plurality rule, sometimes called Single Non-Transferable Vote or SNTV. Bloc Vote gives each voter as many votes as there are seats. The candidates get 12, 12, 13 (or 25), 24, 24, and 19 votes. Again group II wins all. The Limited Vote rule would give each voter 2 votes to cast. Group I could win 1 seat - unless it has a third candidate or Group II concentrates on 3 candidates. This shows the importance of ballot preferences and transfers. The 5 charts below show a whole STV tally turning ballots into reps; 12 ballots add up to 1 rep.
Neighboring candidates have similar opinions so most voters rank them close together. But the 2 interest groups are far apart. Their positions jump from B to R. To play this game, click whichever pile of ballots must transfer. If you click correctly you will jump to the next step of the tally. (If you don't like to play, just scroll down to the next step.) |
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
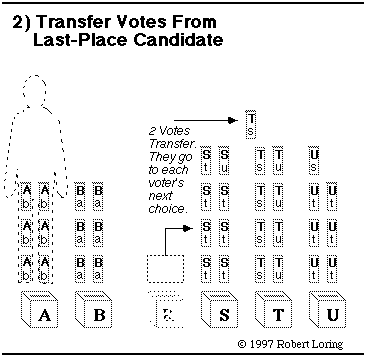
Here's a hint: look for the candidate with the fewest ballots.
Back to chart 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
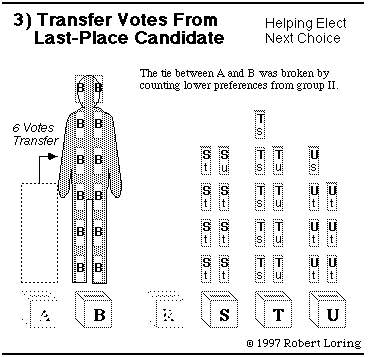
Here's a hint: Candidates A and B each have 6 first-place votes.
You could break this tie with second-place votes of Group II.
Would voters in Group II prefer A or B?
Back to chart 2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
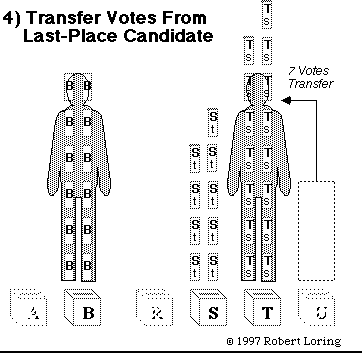
Here's a hint: look for the candidate with the fewest ballots.
Back to chart 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Here's a hint, look for the candidate with excess ballots.
Back to chart 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
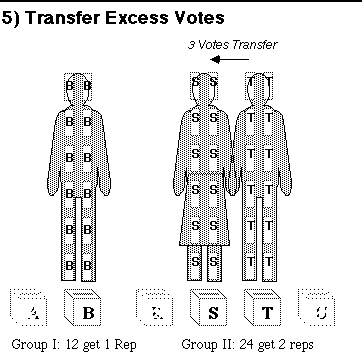
You made it! Way to go. 
Click here to download the STV tally formatted onto 1 page MS Word 4 (Macintosh).
STV is not only for elections. It can organize voters into large groups supporting a variety of one-time resource allocations. For example, the "candidates" above could have been ice cream choices: Lite vanilla, French vanilla; Lite chocolate, Dutch chocolate, Chocolate & chocolate chip, or Mocca chip. The unique chapter on selecting one-time projects and events will show how transferable votes adapt to fair-share spending when the proposals vary in cost.

|
|

 Accurate Democracy
Accurate Democracy